Observe the relative motion of the floating base with respect to the floor. More...
#include <WheelOdometry.h>
Classes | |
| struct | Parameters |
| Observer parameters. More... | |
Public Member Functions | |
| WheelOdometry (const Parameters ¶ms) | |
| Initialize observer. More... | |
| void | read (const Dictionary &observation) final |
| Observe leg contacts. More... | |
| std::string | prefix () const noexcept final |
| Prefix of outputs in the observation dictionary. More... | |
| void | reset (const Dictionary &config) override |
| Reset observer. More... | |
| void | write (Dictionary &observation) final |
| Write outputs, called if reading was successful. More... | |
Detailed Description
Observe the relative motion of the floating base with respect to the floor.
Consider a given wheel \(i \in \{\mathit{left}, \mathit{right}\}\). Assuming the wheel is rolling without slipping on the floor, its velocity is related to that of the base, in the base frame \(B\), by:
\[ \sideset{_B}{} {\begin{bmatrix} v_i^x \\ v_i^y \\ v_i^z \end{bmatrix}} = \sideset{_B}{} {\begin{bmatrix} v^x \\ v^y \\ 0 \end{bmatrix}} + \sideset{_B}{} {\begin{bmatrix} 0 \\ 0 \\ \omega \end{bmatrix}} \times \sideset{_B}{} {\begin{bmatrix} r_i^x \\ r_i^y \\ 0 \end{bmatrix}} + \sideset{_B}{} {\begin{bmatrix} \dot{r}_i^x \\ \dot{r}_i^y \\ \dot{r}_i^z \end{bmatrix}} \]
where \(v_i\) is the linear velocity of the contact point at wheel \(i\), \(v\) is the linear velocity of the base, \(\omega\) is the body angular velocity of the base (in full: the magnitude of the angular velocity from base to world in base, whose direction we assume is aligned with the ground normal), \(r_i\) is the position of the wheel contact point in the base frame, and \(\dot{r}_i\) its time derivative (zero if the hips and knees don't move, non-zero if they do).
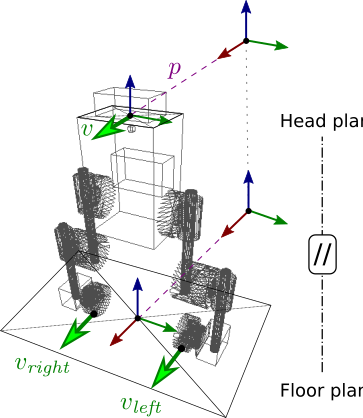
When we infer, all these equations should be satisfied simultaneously. The system is over-determined so we can do it in a least-squares sense.
In this observer, we further assume that \(\omega\) and \(\dot{r}_i\) are zero, so that the kinematics simplify to:
\[ \sideset{_B}{} {\begin{bmatrix} v_i^x \\ v_i^y \end{bmatrix}} = \sideset{_B}{} {\begin{bmatrix} v^x \\ v^y \end{bmatrix}} \]
We then simply compute \(v\) from \(v_i\)'s with an arithmetic average. The relative position of the base with respect to the ground is finally computed by forward integration:
\[ p(T) = \int_{t=0}^T v(t) {\rm d}t \]
The initial time \(t = 0\) in this formula corresponds to touchdown. Odometry is only incremented when at least one wheel is in contact with the ground; its output is stationary when both legs are in the air.
The documentation for this class was generated from the following files:
- upkie/cpp/observers/WheelOdometry.h
- upkie/cpp/observers/WheelOdometry.cpp