State observers available for Upkies. More...

Classes
class	BaseOrientation
	Observe the orientation of the base frame relative to the world frame. More...

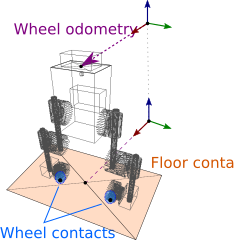
class	FloorContact
	Observe contact between the wheels and the floor. More...

class	HistoryObserver
	Report high-frequency history vectors to lower-frequency agents. More...

class	Observer
	Base class for observers. More...

class	ObserverPipeline
	Observer pipeline. More...

class	WheelContact
	Observe contact between a given wheel and the floor. More...

class	WheelOdometry
	Observe the relative motion of the floating base with respect to the floor. More...

Functions
Eigen::Matrix3d	compute_base_orientation_from_imu (const Eigen::Quaterniond &quat_imu_in_ars, const Eigen::Matrix3d &rotation_base_to_imu, const Eigen::Matrix3d &rotation_ars_to_world)
	Get the orientation of the base frame with respect to the world frame. More...

double	compute_pitch_frame_in_parent (const Eigen::Matrix3d &orientation_frame_in_parent)
	Get pitch angle of a given frame relative to the parent vertical. More...

double	compute_base_pitch_from_imu (const Eigen::Quaterniond &quat_imu_in_ars, const Eigen::Matrix3d &rotation_base_to_imu, const Eigen::Matrix3d &rotation_ars_to_world)
	Get pitch angle of the base frame relative to the world frame. More...

Eigen::Vector3d	compute_base_angular_velocity_from_imu (const Eigen::Vector3d &angular_velocity_imu_in_imu, const Eigen::Matrix3d &rotation_base_to_imu)
	Compute the body angular velocity of the base from IMU readings. More...

void	observe_servos (palimpsest::Dictionary &observation, const std::map< int, std::string > &servo_name_map, const std::vector< ServoReply > &servo_replies)
	Observe servo measurements. More...

void	observe_time (Dictionary &observation)
	Observe time since the epoch. More...

Detailed Description

State observers available for Upkies.

State observation.

Classes